find the points at which two circles intersect

Reference : https://math.stackexchange.com/questions/256100/how-can-i-find-the-points-at-which-two-circles-intersect This can be done without any trigonometry at all. Let the equations of the circles be (x−x1)2+(y−y1)2=r21,

(x−x2)2+(y−y2)2=r22. By subtracting (2) from (1) and then expanding, we in fact obtain a linear equation for x and y; after a little rearranging it becomes −2x(x1−x2)−2y(y1−y2)=(r21−r22)−(x21−x22)−(y21−y22). (If the circles intersect, this is the equation of the line that passes through the intersection points.) This equation can be solved for one of x or y; let's suppose y1−y2≠0 so that we can solve for y: y=−x+…. Substituting this expression for y into (1) or (2) gives a quadratic equation in only x. Then the x-coordinates of the intersection points are the solutions to this; the y-coordinates can be obtained by plugging the x-coordinates into (3).

Easy solution is to consider another plane such that the centers are along an axis.

The distance between the centers of the circles is given by

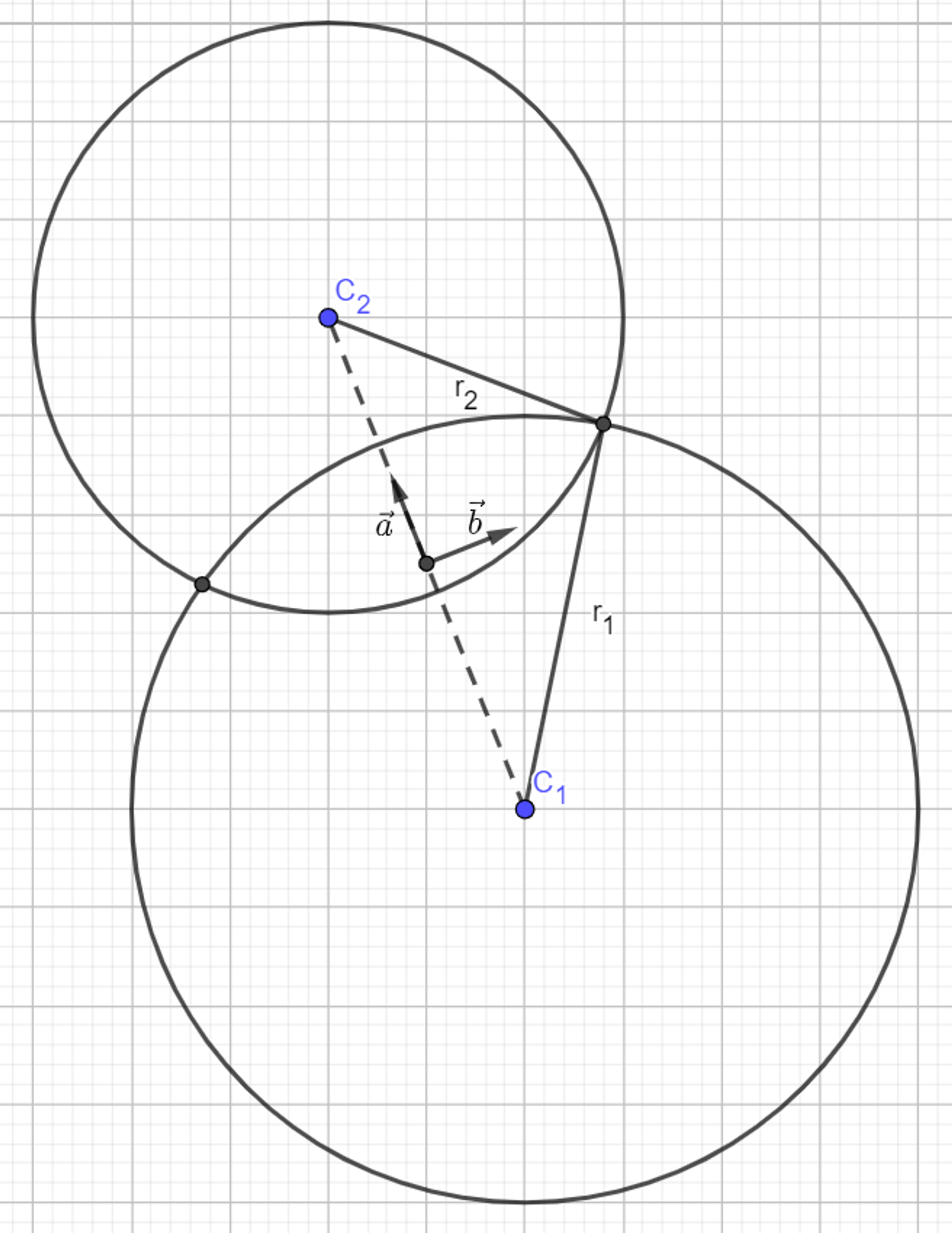
Whence

The intersection points are given by where R is the distance between the centers of the circles.

A nice way to look at this is to first consider the case when one point is at the origin and the other lies on the x-axis. Let the points be at (0,0), (d,0) and the radii be r1, r2. The two equations simplify to x2+y2=r21

and (x−d)2+y2=r22 Use the first to find y2 and substitute in the second. (x−d)2+r21−x2=r22 expand and simplify −2xd+d2+r21=r22 so x= and from Pythagorus y=√. This part came from mathworld.

For the general position case with points (x1,y1) (x2,y2) let d=√l=h=√

Now (,) (,−) are two orthogonal unit vectors and we can rotate and translate to get the general solution x=(x2−x1)±(y2−y1)+x1,y=(y2−y1)∓(x2−x1)+y1.

(x−x2)2+(y−y2)2=r22

They intersect only iff |r1−r2|≤|C1−C2|≤|r1+r2|, where |C1−C2| is the distance between the two centers. If equality holds, the circles touch and there is one solution. For strict inequalities, they intersect and they have two solutions.

Just solve the system of equations. Suppose that x0 is a point on the first circle. Then, its parametric representation is x0=(x1+r1cosθ,y1+r1sinθ) for some θ. If x0 also lies on the second circle, which will make it a point of intersection, it must also satisfy the equation of the second circle i.e. (x0−x2)2+(y0−y2)2=r22

Substitute the parametric form, and find out the value(s) of θ.

Solution to Example 1:

Multiply all terms in the first equation by -1 to abtain an equivalent equation and keep the second equation unchanged

We now add the same sides of the two equations to obtain a linear equation

Which may be written as

We now substitute the values of y already obtained into the equation x=9−4y to obtain the values for x as follows

following the very nice hint of arkeet you can after defining a,b,c,g,h using rc1,zc1,rc2,zc2, as the center point of the circles and R1 and R2 their radii and assuming that rc2!=rc1 (the case where rc2=rc1 can be also done in the manner or arkeet, however the present assumption was useful to me)

g = (zc2 - zc1)/(rc2 - rc1); h = (R1R1-R2R2 + zc2zc2 - zc1zc1 + rc2rc2 - rc1rc1 )/(2*(rc2 - rc1));

a = (gg+ 1); b = -2gh + 2grc1 - 2zc1; c = hh -2hrc1 + rc1rc1 + zc1zc1 - R1R1;

zplus = (-b +sqrt(bb-4ac)) / (2a); zminus = (-b -sqrt(bb-4ac)) / (2a); and rplus = -gzplus+h; rminus = -gzminus+h;

you can test this by verifying that the intersection points do lie on the 2 circles.